Publications
If you’d just like to see an out-of-context list of my publications, choose one of these routes:
- Arxiv’s list of my papers
- Google Scholar’s view of things I’ve written or contributed to
- My CV (available from this page)
Keep scrolling to see a number of my papers in the context of their projects.
Current Projects
Fast Evaluation of 2D/3D Layer Potentials at a High Order of Accuracy (“Quadrature by Expansion”)
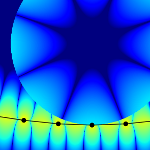
Integral equation methods for the solution of partial differential equations, when coupled with suitable fast algorithms, yield geometrically flexible, asymptotically optimal and well-conditioned schemes in either interior or exterior domains. The practical application of these methods, however, requires the accurate evaluation of boundary integrals with singular, weakly singular or nearly singular kernels. We have developed a systematic, high-order approach that works for any singularity (including hypersingular kernels), based only on the assumption that the field induced by the integral operator is locally smooth when restricted to either the interior or the exterior. Discontinuities in the field across the boundary are permitted. The scheme, denoted QBX (quadrature by expansion), is easy to implement and compatible with fast hierarchical algorithms such as the fast multipole method. We are currently developing this integration and practically applicable, fast solvers based on QBX.
Collaborators: Alex Barnett, Leslie Greengard, Michael O’Neil.
- AK, A. Barnett, L. Greengard, M. O’Neil. Quadrature by Expansion: A New Method for the Evaluation of Layer Potentials. Submitted. arxiv
Frequency-domain electromagnetics (w/applications)

(Details to follow)
Collaborators: Leslie Greengard, Zydrunas Gimbutas, Alexej Jerschow (NYU chemistry), Felipe Vico, Michael O’Neil, Charlie Epstein
- C. Epstein, Z. Gimbutas, L. Greengard, AK, M. O’Neil. A consistency condition for the vector potential in multiply-connected domains Submitted. arxiv
Programming Tools for Parallel Architectures

Graphics Processing Units (GPUs) offer tremendous potential for performance and efficiency. However, exploiting this potential can be challenging, as one must adapt to the specialized and rapidly evolving computing environment currently exhibited by GPUs. One way of addressing this challenge is to embrace better techniques and develop tools tailored to their needs. This article presents one simple technique, GPU run-time code generation (RTCG), and PyCUDA, an open-source toolkit that supports this technique. In introducing PyCUDA, I propose the combination of a dynamic, high-level scripting lan- guage with the massive performance of a GPU as a compelling two-tiered computing platform, potentially offering significant performance and productivity advantages over conventional single-tier, static systems.
- AK, Nicolas Pinto, Yunsup Lee, Bryan Catanzaro, Paul Ivanov, Ahmed Fasih. PyCUDA: GPU Run-Time Code Generation for High-Performance Computing. (Parallel Computing, Volume 38, Issue 3, March 2012, Pages 157–174, arxiv, Brown SC Report)
Viscous Shock Capturing for Time-Explicit GPU DG
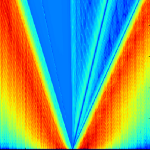
Many important physical problems that could profitably be solved using the GPU DG solvers above can develop discontinuities during their solution time. These discontinuities, due to issues like the Gibbs phenomenon, can be troublesome for high-order solvers. An additional shock capturing component that we have designed to specifically address the needs of GPU-based computation allows the successful treatment of such problems using GPU DG.
Collaborators: Jan Hesthaven (Brown), Tim Warburton (Rice)
- AK, Tim Warburton, Jan Hesthaven. Viscous Shock Capturing in a Time-Explicit Discontinuous Galerkin Method. (MMNP Volume 6, 2011, pages 57-83, arxiv)
DG on GPUs

Discontinuous Galerkin methods are rather arithmetically intense, and they access computational data in a mostly local and ordered fashion. It is therefore natural to ask whether DG would be a good fit for a the massively parallel computation capabilities of moden graphics processing units (GPUs). Working closely with Tim Warburton at Rice, I found that a practical, DG-based 3D Maxwell solver can outperform a current-generation CPU by factors between 40 and 60. We are presently extending our methods towards multi-GPU parallelism and more challenging equations.
Collaborators: Jan Hesthaven (Brown), Tim Warburton (Rice)
- AK, Tim Warburton, Jeff Bridge, Jan S Hesthaven, Nodal Discontinuous Galerkin Methods on Graphics Processors. Journal of Computational Physics, Volume 228, Issue 21, 20 November 2009, Pages 7863-7882. (arXiv, Brown SC Report, JCP)
Multi-Rate Adams-Bashforth Methods
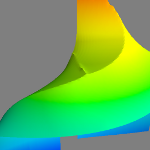
Most time-domain simulations involve processes on a number of different time scales. In explicit time marching schemes, the fastest processes limit the maximal size of the time step, necessitating that slower processes use an unnecessarily small time step. Multi-rate schemes avoid this waste. I derive a new classification of multi-rate Adams Bashforth methods and present initial stability data.
Collaborators: Jan Hesthaven (Brown), Tim Warburton (Rice), Andreas Stock (Stuttgart)
(pub. in prep.)
Past Projects
High-Order Unstructured Particle-in-Cell
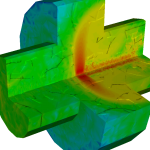
For many problems in Plasma physics, the Particle-in-Cell or “PIC” method is the only computationally feasible method of simulation. However, few existing PIC codes take advantage of the features of modern EM solvers, such as the benefits offered by high-order accurate approximations and unstructured meshes. My goal is to find out what it takes to develop an advanced PIC solver that leverages these (and other) recent advances. We hope that this solver will be able to extend the reach of PIC simulations to areas where very long time integration or very high accuracy is desired. If you’d like to get a visual idea of what I’m doing, you may view my research gallery.
Collaborators: Jan Hesthaven (Brown), Yong-Chul Chae (ANL), Jonathan Neudorfer (Stuttgart)
Dissertation
Much of my PhD research is summarized in my PhD thesis. Grab it here:
- PhD Thesis (May 2010, PDF)
Computation of Maximally-Localized Wannier Functions
This is the project I pursued for my Diplom thesis at Universität Karlsruhe in Germany. The idea here is to compute specialized basis functions allowing the efficient computation of dispersion relations for large photonic crystals. My approach involved a second-order finite-element-based eigensolver and a CG-derived minimization procedure.
- Thesis (English, PDF). A gentler introduction is also available on the talks page.
Advisor: Willy Dörfler (Karlsruhe)